개발계발 - 1

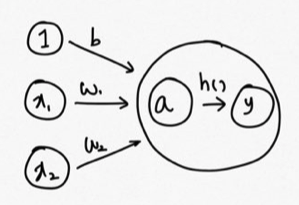
지난 챕터에서는 데이터를 예측하고 예측 값에 대한 손실함수 구하기를 살펴보았다. 지난 챕터 바로가기 : https://myphiloprogramming.tistory.com/22 다음 순서를 계속 진행해보자. 4. 경사하강법으로 가중치 값 개선하기 우리는 손실 함수 값을 줄여나감으로써 최적의 매개변수를 찾는다. 손실 함수 값을 줄이는 방법으로는 경사하강법을 사용하는데, 적용하기 전에 그 방법을 이해해보자. 먼저, 손실 함수값을 좌표 위에 찍어서 현재 위치를 확인한다. 적기로는 좌표 위에 점을 찍는다고 했지만, 실제로 차원은 가중치 매개변수 개수 만큼 있기 때문에 그릴수도, 그래프의 모양을 확인할 수도 없다. 적당히 이해하기로는 x축은 가중치 매개변수 개수 만큼있고 y축은 손실함수 값이 된다. 그림으로 나..

이번 챕터에서는 신경망 학습 방법에 대해 알아본다. 우리는 "5"라고 쓴 손글씨 이미지를 입력하면 컴퓨터가 "5"라고 인식하는 모델을 만들고 싶다. 이 모델을 만들기 위해서 신경망을 학습시킬 것이다. (이를 모델링이라고도 한다.) 신경망은 학습을 통해 손글씨 값을 가장 잘 인식하는 가중치와 편향의 최적값을 찾아준다. 우리는 최적값을 가지고 숫자를 얼마나 잘 맞추는지 성능을 테스트 할 것이다. 우리가 사용할 데이터는 MNIST 패키지의 손글씨 이미지이다. 이미지는 다음과 같다. 손글씨로 쓴 숫자 5의 이미지이다. 이미지를 넘파이 배열로 변환하여 학습시킬 것이다. 해당 이미지는 28 * 28 사이즈로, 픽셀별로 쪼개어 배열로 만든다. 회색조 이미지에서 각 픽셀은 색상에 따라 0에서 255까지의 값을 취한다...

앞선 글에서 퍼셉트론, 가중치, 편향, 비선형, 다중퍼셉트론을 살펴보았다. 퍼셉트론 식을 구현하는 데 있어 가중치와 편향을 적절한 값으로 직접 설정했다. 그러나 층이 많아질수록 직접 설정할 수 없을 것이다. 신경망은 학습을 통해 가중치, 편향에 대한 적절한 값을 찾아준다. 신경망 신경망 네트워크는 입력층 - 은닉층 - 출력층으로 구성되는데, 은닉층의 경우 처리 과정을 확인할 수 없다. 신경망의 구조는 다층 퍼셉트론과 유사하다. 퍼셉트론에서 신경망으로 나아가 보자. 앞서 정의한 퍼셉트론 식을 다시 보자. x1,x2는 입력신호, w1,w2는 가중치, b는 편향이다. 이 3가지를 네트워크로 나타내보자. 익숙한 그림이지만 편향이 추가됐다. 이 그림은 위 퍼셉트론 식을 1*b + w1*x1 + w2*x2라고 풀어..

퍼셉트론 알고리즘 퍼셉트론은 딥러닝의 기원이 되는 알고리즘으로, 다수의 신호를 입력으로 받아 처리한 후 하나의 신호를 출력한다. 좀 더 구체적으로 설명하면 입력 받은 신호에 가중치를 곱해서 신호의 총합이 정해진 한계(임계값)를 넘어설 때만 1을 출력한다. 이 동작 원리를 수식으로 나타내면 아래와 같다. 위 식의 x1,x2는 입력신호, w1,w2는 가중치를 나타낸다. 그리고 계산식의 합이 임계값(θ)를 넘는 경우에만 1을 출력한다. 입력신호(x1,x2)는 우리가 결정할 수 없는, 그저 받는 값이지만, 가중치와 임계값은 조절할 수 있다. 계산식에서 가중치(w1,w2)로 입력신호의 중요도를 조절하고, 임계값으로 얼마나 쉽게 1을 출력할 것인지를 설정한다. 가중치는 높을수록 입력신호의 값이 커져 영향력이 커지게..