퍼셉트론 알고리즘
퍼셉트론은 딥러닝의 기원이 되는 알고리즘으로, 다수의 신호를 입력으로 받아 처리한 후 하나의 신호를 출력한다.
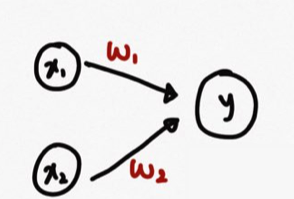
좀 더 구체적으로 설명하면 입력 받은 신호에 가중치를 곱해서 신호의 총합이 정해진 한계(임계값)를 넘어설 때만 1을 출력한다. 이 동작 원리를 수식으로 나타내면 아래와 같다.

위 식의 x1,x2는 입력신호, w1,w2는 가중치를 나타낸다. 그리고 계산식의 합이 임계값(θ)를 넘는 경우에만 1을 출력한다.
입력신호(x1,x2)는 우리가 결정할 수 없는, 그저 받는 값이지만, 가중치와 임계값은 조절할 수 있다. 계산식에서 가중치(w1,w2)로 입력신호의 중요도를 조절하고, 임계값으로 얼마나 쉽게 1을 출력할 것인지를 설정한다. 가중치는 높을수록 입력신호의 값이 커져 영향력이 커지게 되며 낮을수록 그 입력신호는 영향력이 작아진다. 그리고 임계값이 낮을수록 1은 쉽게 출력될 것이다. 이처럼 가중치와 임계값은 각 신호가 결과에 주는 영향력을 조절한다.
이번에는 임계값을 좌변으로 옮겨 아래와 같이 수식으로 나타낼 수 있다.
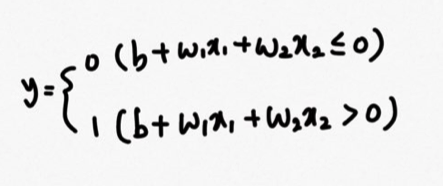
임계값을 좌변으로 넘기고(b) 임계값을 더한 계산식의 합이 0이 넘는 경우에만 1을 출력한다. 항상 계산식이 0보다 크면 1을 출력하므로 이해하기 훨씬 간편하다. 우리는 이 b를 편향이라고 부른다.
논리 회로 구현하기
앞서 작성한 퍼셉트론 식으로 논리 회로를 구현해 보자. 논리 회로는 하나 이상의 논리 값이 들어오면 게이트에 따라 출력 논리 값을 반환한다. 게이트로는 AND게이트, OR게이트, XOR게이트, NAND게이트를 살펴 볼 것이다.
AND 게이트
아래 표는 AND논리회로의 진리표이다. 입력 값이 둘 다 1인 경우에만 1을 반환한다.
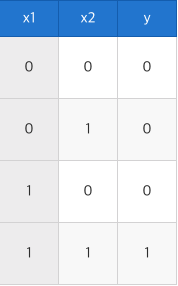
이 진리표를 퍼셉트론으로 표현하려면 가중치와 편향을 어떻게 설정해야 할까?
입력값을 x1, x2에 대한 가중치를 w1, w2라고 했을 때 (w1,w2,b)는 (0.5,0.5,-0.7), (1.0,1.0,-1.0)등이 될 수 있을 것이다.
이처럼 가중치와 편향을 적절히 하여 AND 논리회로를 구현해보자.
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0 :
return 0
else:
return 1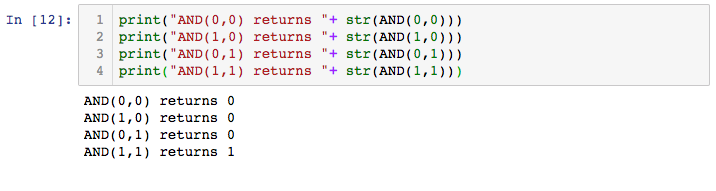
OR, NAND게이트
다음으로 OR, NAND게이트도 마저 구현해 본다. OR게이트는 입력값이 모두 0인 경우를 제외하고 1을 반환하고 NAND게이트는 입력값이 모두 1인 경우에 0을 반환한다.

def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0 :
return 0
else:
return 1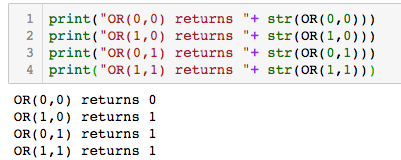
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0 :
return 0
else:
return 1
XOR 논리회로는?
아래는 XOR논리회로의 진리표이다.

XOR 논리회로는 x1,x2가 다른 경우에만 1을 반환한다. 마찬가지로 코드로 구현하려니 앞서 다른 논리회로와 같은 방식으로는 구현할 수가 없다. 왜 그럴까? 그래프로 살펴보자


먼저 OR진리표를 그래프로 나타낸 것이다. OR그래프는 0과 1을 분리하기 위해서 1차식으로 나타낼 수 있다. AND와 NAND논리회로 역시 1차식으로 나타낼 수 있다. 직접 그려보기 바란다.
다음으로 XOR그래프를 살펴보자


XOR 그래프는 0과 1을 분리하기 위해 1차식으로 구현할 수 없다. 1과 0을 분리하기 위해서는 곡선이 들어가게 된다.
정리하면 AND,OR,NAND가 선형 문제인 반면에 XOR은 비선형 문제이므로 1차식으로 문제를 해결할 수 없는 것이다.
비선형 문제 해결하기 : 다층 퍼셉트론
그렇다면 퍼셉트론 식만으로 비선형 문제를 어떻게 해결해야 할까? XOR같은 비선형 문제를 해결하는 것이야 말로 퍼셉트론의 진가이다. 1차식 만으로 해결할 수 없는 비선형 문제는 층을 쌓아 해결한다. 이것을 다층 퍼셉트론이라고 부른다.
다층 퍼셉트론을 그림으로 나타내면 다음과 같다.
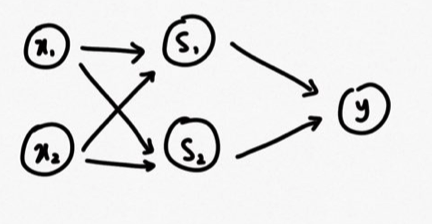
하나의 처리과정을 한 층이라고 부른다. 해당 퍼셉트론은 처리 과정이 2개이므로 2층 퍼셉트론이다. 그림을 설명하면 입력신호(x1,x2)에 대한 처리를 하고 처리된 신호(s1,s2)를 다시 처리하여 y를 출력한다. 기존의 1층 처리 방식과 달리 처리된 것을 다시 처리하여 출력한다. 이 방식을 XOR에 적용해보자. 먼저 XOR 방식을 해결하기 위한 처리 과정은 아래와 같다.
| x1 | x2 | s1 | s2 | y |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
입력 신호(x1, x2)는 다른 논리회로와 같다. 다만 입력신호를 NAND로 처리한 s1과 OR로 처리한 s2(1층)를 다시 AND 신호(2층)로 처리한다. 이를 수식으로 나타내면 아래와 같다.
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
이처럼 퍼셉트론은 층을 쌓아 더 다양한 것을 표현할 수 있다.
'프로젝트 > 딥러닝' 카테고리의 다른 글
| [CH.4]신경망 학습하기-2 (경사하강법) (0) | 2020.02.09 |
|---|---|
| [CH.4]신경망 학습하기-1 (손실함수, 교차엔트로피오차) (1) | 2020.02.02 |
| [CH.3]딥러닝의 시작2, 신경망 - 활성화 함수 (0) | 2020.01.25 |